学習

電気と磁気の世界における場の捉え方について学習しました。 場とは何か？ ＊気温の全国分布図の例＊ 札幌　２７℃ 東京　２４℃ ：温度の場について： 場所によって温度が決まっている ↓ 空間の座標の関数 ...

例：製品１キロあたり１万円の利益を見込む場合 →１００キロ生産すれば１００万円の利益見込み 生産量をx軸　利益をy軸にとると右上がりの直線グラフとなる。（線形関係） ・もし大量生産が見込めるのなら単位 ...

今回は結果の生起確率について着目します。 ＊主観確率 ・繰り返しのない事象の生起確率 →　生起頻度から得られない →　主観的な判断に基づく　・・・　主観確率 →　前々回でやった雨が降る確率とか採掘成功 ...

～　期待効用最大化原理　～ 期待効用が最大となる決定が、最適な決定であると言えるためにはいくつかの満たすべき前提条件がある。 ＊結果 ・行動aを選択し、状態Θが生じた結果y=(a,Θ) ［前提１］：多 ...

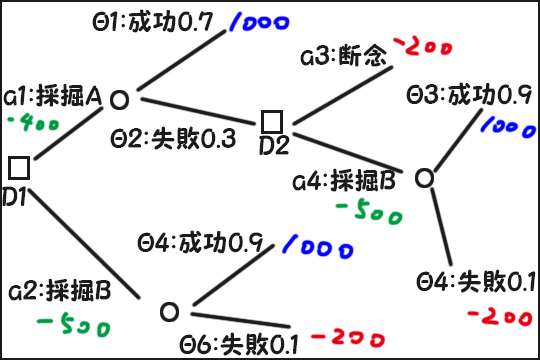
引き続き、統計的な意思決定について学習しました。 前回の傘よりも少し複雑な意思決定について、効用を最大化する方法を考えます。 多段階決定問題 ・資源の採掘に成功したら１０００億円の収入。 ・資源の採掘 ...

統計的な意思決定について学習しました。 この知識は日常生活で役に立つような気がします。＾０＾ 健康や株価など不確実性が伴う状況において、合理的な決定を行うには統計的アプローチが有効であると考えられる。 ...

前回まででストレスコーピングの方法を学びました。 今回は生活習慣を振り返り、リラクセーションをすることによって心身を健全にする方法を学習しました。 3. 生活習慣を振り返る ：セルフワーク　その３： ...

前回はストレスコーピング実践前の下準備としてストレスの原因を整理しました。 今回はストレスコーピングの方法を学びました。 2. ストレスコーピングの方法を考える *step1.状況* →　プロジェクト ...

ストレスコーピングについて学習しました。 ストレスコーピングとはストレスを受けたときの対処方法のことです。 ストレスコーピングの実践 １．　ストレスの原因を整理する ～　職場のストレス要因に気づくため ...

引き続き、錯覚ついて学びました。 レオン・フェスティンガー著　「予言がはずれるとき」 終末予言教祖さま 「１９９９年に人類は滅亡する！」　ΩΩΩ<な、なんだってー!? ↓ 滅亡しませんでした　( ...